Сказать "Спасибо"

Метод введения параметра для уравнений первого порядка, не разрешенных относительно производной.

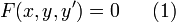
$F(x, y, y')=0~~~~~(1)$

-общий вид дифференциального уравнения первого порядка, не разрешенного относительно производной. Здесь

$F (x, y, p)$ - заданная непрерывная функция в некоторой непустой области $G$ евклидового пространства $\mathbb{R}^3$ с декартовыми прямоугольными координатами $x, p, y$ ; $x$ - аргумент; $y = y (x)$ - неизвестная функция.

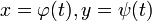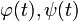Вектор функция $x=\varphi(t), y=\psi(t)$ , где $t$ принадлежит промежутку $I\in R$ и $\varphi(t), \psi(t)$ - непрерывно дифференцируемы на $I$ , причем 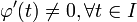$\varphi'(t)\ne 0, \forall t\in I$ , если при подстановке 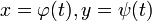$x=\varphi(t), y=\psi(t)$ в уравнение (1) получаем тождество

$F\left[\varphi(t),\psi(t),\frac{\psi'(t)}{\varphi'(t)}\right]\equiv 0$

параметрическое решение (1) допускает явное представление $y = ω(x)$ .

Положим $y' = p$ и рассмотрим смешанную систему уравнений

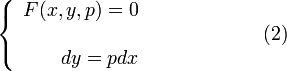
$\left\{ \begin{array}{rcl} F(x, y, p)=0 \\ & &~~~~~~~~~~~~~~(2)\\ dy=pdx \end{array} \right.$

Покажем, что уравнение (1) эквивалентно системе (2), т.е каждое решение уравнения (1) определяет решение системы (2) и наоборот.

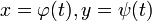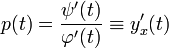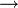Действительно, если $x=\varphi(t), y=\psi(t)$ является параметрическим решением (1), то $p(t)=\frac{\psi'(t)}{\varphi'(t)}\equiv y_x'(t)$ . Отсюда $dy(t)\equiv p(t)dx(t)$ и $F[\varphi(t),\psi(t),p(t)]\equiv 0$ . (1) $\to$ (2)

Обратное пусть 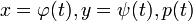$x=\varphi(t), y=\psi(t), p(t)$ удовлетворяют системе (2), находим из второго 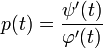$p(t)=\frac{\psi'(t)}{\varphi'(t)}$ , а из первого следует что $F\left[\varphi(t),\psi(t),\frac{\psi'(t)}{\varphi'(t)}\right]\equiv 0$ .

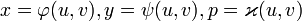Уравнение $F (x, y, p) = 0$ определяет в $\mathbb{R}^3$ такую гладкую поверхность $S$ , для которой известно также и параметрическое представление. Это значит, что существуют такие непрерывно дифференцируемые функции $x=\varphi(u,v), y=\psi(u,v), p= \varkappa(u,v)$ , в некоторой области $Ω$ плоскости с декартовыми прямоугольными координатами $u, v$ , для которых положительна сумма квадратов якобианов:

$\left[\frac{D(x,y)}{D(u,v)}\right]^2+\left[\frac{D(y,p)}{D(u,v)}\right]^2+\left[\frac{D(p,x)}{D(u,v)}\right]^2 > 0$

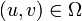и $F[\varphi(u,v), \psi(u,v),\varkappa(u,v)]\equiv 0$ для всех $(u, v)\in \Omega$ .

Второе уравнение системы (2) дает уравнение вида

$\frac{\partial \psi}{\partial u}du+\frac{\partial \psi}{\partial v}dv\equiv\varkappa(u, v)\left[\frac{\partial\varphi}{\partial u}du+\frac{\partial\varphi}{\partial v}dv\right]$

или

$\left[\frac{\partial\psi}{\partial u}-\varkappa\frac{\partial\varphi}{\partial u}\right]du+\left[\frac{\partial \varphi}{\partial v}-\varkappa\frac{\partial\psi}{\partial v}\right]dv=0$

Получилось уравнение первого порядка в симметричной форме.

Сказать "Спасибо"

Метод введения параметра для уравнений первого порядка, не разрешенных относительно производной.

Комментарии