Сказать "Спасибо"

Теорема существования и единственности решения задачи Коши для нормального уравнения первого порядка.

Нормальная система в векторных обозначениях примет вид

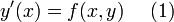
$y'(x)=f(x, y)~~~~(1)$

где 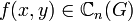$f(x, y)\in \mathbb{C}_n(G)$ .

Определение. Вектор-функция 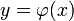$y=\varphi(x)$ называется решением нормальной системы (1) на промежутке 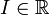$I\in \mathbb{R}$ , если:

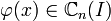
1. $\varphi(x) \in \mathbb{C}_n(I)$

2. $(x, \varphi(x)) \in G$

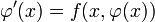
3. $\varphi'(x)=f(x, \varphi(x))$

Рассмотрим начальное условие

$y(x_0)=y_0,~~~~(x_0, y_0)\in G~~~~~(2)$

Точка $(x 0, y 0)$ называется начальной точкой, а ее координаты $x 0, y 0$ называются начальными данными.

Определение. Задача нахождения решения нормальной системы (1), удовлетворяющего начальному условию (2), называется задачей Коши.

Система уравнений вида

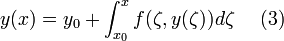
$y(x)=y_0+\int_{x_0}^{x}f(\zeta, y(\zeta))d\zeta~~~~(3)$

где 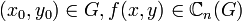$(x_0, y_0)\in G, f(x, y)\in \mathbb{C}_n(G)$ , назыается системой интегральных уравнений.

Вектор-функция 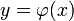$y=\varphi(x)$ называется решением на промежутке 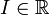$I\in \mathbb{R}$ системы (3), если:

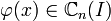
1. $\varphi(x) \in \mathbb{C}_n(I)$

2. $(x, \varphi(x)) \in G$

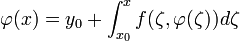
3. $\varphi(x)=y_0+\int_{x_0}^{x}f(\zeta, \varphi(\zeta))d\zeta$

Лемма об эквивалентности. Вектор-функция 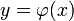$y=\varphi(x)$ - решение задачи Коши (1) при условии (2) тогда и только тогда, когда 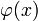$\varphi(x)$ решение системы интегральных уравнений (3).

Теорема существования и единственности решения задачи Коши.

Пусть вектор-функция 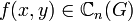$f(x, y)\in \mathbb{C}_n(G)$ удовлетворяет на каждом компакте области $G$ условию Липшица

$\exists L > 0: \forall (x, y_1),(x, y_2)\in G |f(x, y_1)-f(x, y_2)|\leq L|y_1-y_2|$

Тогда:

1) найдется такое $δ > 0$ , что при $| x - x 0 |$ решение задачи Коши (1) при условии (2) существует,

2)решение задачи Коши единственно

В силу леммы об эквивалентности доказательство теоремы сводится к доказательству существования и единственности решения системы интегральных уравнений (3).

A)Существование

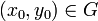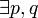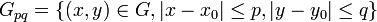Поскольку $(x_0, y_0)\in G$ и $G$ - открытое множество, то $\exists p, q$ что замкнутый цилиндр $G_{pq}=\left\{(x, y)\in G,|x-x_0| \leq p, |y-y_0| \leq q \right\}$ принадлежит $G$ . В силу того, что цилиндр $G p q$ компакт то

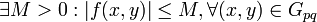
$\exists M > 0 :|f(x, y)|\leq M, \forall (x, y)\in G_{pq}$

Будем строить решение системы интегральных уравнений (3) методом приближений Пикара при $| x 0 - x | < δ$ , где 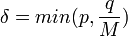$\delta=min(p, \frac{q}{M})$ . Определим последовательные приближения следующим рекурентным образом при $|x-x_0| \leq \delta$ :

$y_0(x)=y_0,~~~~~y_{i+1}=y_0+\int_{x_0}^{x}f[\zeta, y_{i}(\zeta)]d\zeta$

ясно, что каждая $y i (x)$ непрерывна при $(x, y)$ , и что $(x, y_i(x))\in G_{pq}$

$|y_1(x)-y_0(x)|=\left|\int_{x_0}^{x}f[\zeta, y_0]d\zeta\right|\leq \left|\int_{x_0}^{x}|f[\zeta, y_0]|d\zeta\right|\leq M |x-x_0|\leq M\delta \leq q$

Как известно из курса анализа, равномерная сходимость функционального ряда 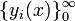$\{y_i(x)\}_{0}^{\infty}$ эквивалентна равномерной сходимости ряда вида

$y_0(x)+\sum_{i=0}^{\infty}[y_{i+1}-y(x)]$

докажем оценку

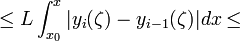
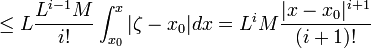
$|y_{i+1}(x)-y_{i}(x)|\leq\int_{x_0}^{x}|f[\zeta,y_{i}(\zeta)]-f[\zeta,y_{i-1}(\zeta)]|dx\leq$ $\leq L\int_{x_0}^{x}|y_{i}(\zeta)-y_{i-1}(\zeta)|dx\leq$ $\leq L\frac{L^{i-1}M}{i!}\int_{x_0}^{x}|\zeta-x_0|dx=L^iM\frac{|x-x_0|^{i+1}}{(i+1)!}$

По теореме Вейршрасса получаем, что

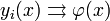
$y_i(x)\rightrightarrows \varphi(x)$

$\int_{x_0}^{x}f[\zeta,y_i(\zeta)]d\zeta\rightrightarrows\int_{x_0}^{x}f[\zeta,\varphi(\zeta)]d\zeta$

Единственность следует из леммы Гронуолла.

Сказать "Спасибо"

Теорема существования и единственности решения задачи Коши для нормального уравнения первого порядка.

Комментарии